カメラの外部パラメータを推定する（2Dカメラ）

カフェチームの山本です。

現在、カフェチームでは、商品にいる人物を撮影し、機械学習を用いて人物の骨格を検出することで、どの商品を取り出したかを判定しています。そのために、Depthカメラ（RGB画像とDepth画像を取得できるカメラ）を用いてユーザを撮影し、骨格の3次元位置を推定しています。

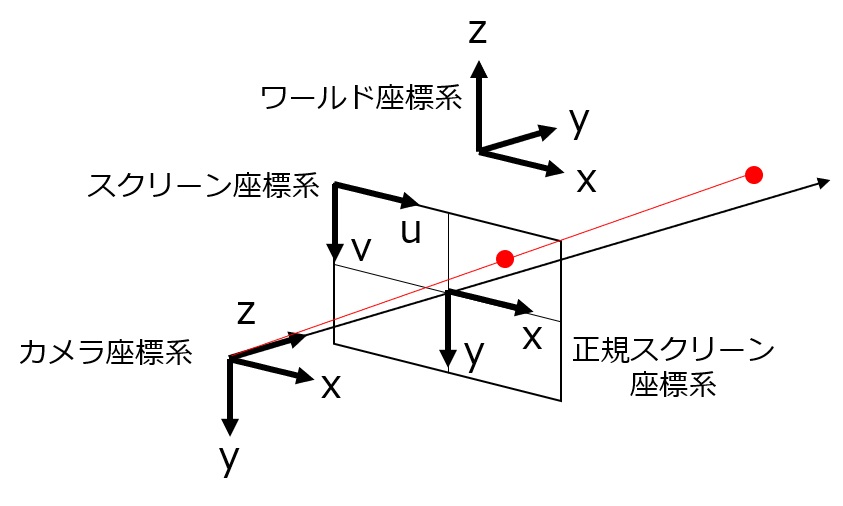
今後、エッジ側の機器のコストを下げるために、通常のカメラ（RGB画像のみ）を用いることを検討しています。そのためには、RGB画像のみで、カメラのキャリブレーション（外部パラメータを推定する）をする必要があります。以前の記事では、Depthカメラを前提としていたため、画像中の「スクリーン座標+奥行き」と、空間の「ワールド座標」との間を変換するための計算方法を記載しました。

カメラの外部パラメータ行列を最小二乗法で推定する

今回は、RGBカメラを用いること考え、画像中の「スクリーン座標」と、空間の「ワールド座標」との間の変換する計算方法について記載します。

お詫び

本ページの数式が正しく表示されていません。現在、修正中です。数式まで見たい方はこちらのページをご覧ください。

カメラの外部パラメータを推定する（2Dカメラ）

０．定義

今回用いる定義などは、以下の記事のものをそのまま使用します。

画像の座標を空間の座標に変換する

• t：スクリーン座標系におけるカメラの並進ベクトル
• R：スクリーン座標系におけるカメラの回転行列
• K：カメラの内部パラメータ行列
• cw：ワールド座標系における座標
• cc：カメラ座標系における座標
• (us, vs)：スクリーン座標系における座標
• zs：カメラから見た奥行き

[latex]R = \left( \begin{matrix} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} \end{matrix} \right)[/latex]

[latex]t=\left( \begin{matrix} t_{1} \ t_{2} \ t_{3} \end{matrix} \right)[/latex]

[latex]K = \left( \begin{matrix} f_{w} & 0 & c_{x} \ 0 & f_{h} & c_{y} \ 0 & 0 & 1 \end{matrix} \right)[/latex]

[latex]c_{w} =\left( \begin{matrix} x_{w} \ y_{w} \ z_{w} \end{matrix} \right)[/latex]

[latex]c_{c} =\left( \begin{matrix} x_{c} \ y_{c} \ z_{c} \end{matrix} \right)[/latex]

[latex]c_{w} = \left[ R | t \right] \left( \begin{matrix} c_{c} \ 1\end{matrix} \right)[/latex]

[latex]c_c = z_s K^{-1} \left( \begin{matrix} u_s \ v_s \ 1 \end{matrix} \right)[/latex]

書き直すと、以下のようになります。

[latex]\left( \begin{matrix} x_c \ y_c \ z_c \end{matrix} \right) = z_s K^{-1} \left( \begin{matrix} u_s \ v_s \ 1 \end{matrix} \right)[/latex]

[latex]\left( \begin{matrix} x_w \ y_w \ z_w \end{matrix} \right) = \left[ \begin{matrix} r_{11} & r_{12} & r_{13} & t_{1} \ r_{21} & r_{22} & r_{23} & t_{2} \ r_{31} & r_{32} & r_{33} & t_{3} \end{matrix} \right] \left( \begin{matrix} x_c \ y_c \ z_c \ 1 \end{matrix} \right)[/latex]

以前の記事と同様に、内部パラメータは既知であるものとして、外部パラメータ（R、t）を推定します。

１．計算

使用データ

前回と同様に、UnrealEngineで作成したシーンから、座標のセット（次節のスクリプト中のCOORD_SET_FOR_CALIBと、COORD_SET_FOR_TEST）を作成しました。カメラのパラメータは以下の通りです。

• カメラ座標： x：392, y：336, z：234
• 画角（fov）：90°
• 解像度横：1280[px]
• 解像度縦：720[px]
• 光軸：中心

パラメータ推定方法：solvePnPを使う

結論から書くと以下のようにすることで、外部パラメータの推定と、推定したパラメータを用いた座標変換ができます。

用意した画像座標と空間座標のセットを、cv2.solvePnP関数に入力することで、外部パラメータを推定します。推定したパラメータと、空間座標をcv2.projectPoints関数に入力することで、画像座標に変換できます。

import cv2
import numpy as np
import math

# const
COORD_SET_FOR_CALIB = [
    # uvz(screen cood), xyz(unrealengine coord)
    ([663, 306], [560, 500, 100]),
    ([871, 313], [500, 560, 100]),
    ([776, 366], [500, 500, 100]),
    ([758, 263], [560, 560, 100]),
    ([762, 469], [500, 500, 50]),
    ([898, 562], [440, 500, 50]),
]

COORD_SET_FOR_TEST = [
    # uvz(screen cood), xyz(unrealengine coord)
    ([1022, 376], [440, 560, 100]),
    ([935, 453], [440, 500, 100]),
    ([748, 354], [560, 560, 50]),
    ([849, 408], [500, 560, 50]),
    ([661, 402], [560, 500, 50]),
    ([978, 481], [440, 560, 50]),
]

FOV = 90
PW = 1280
PH = 720

# calc Camera Intrinsic Parameter Matrix
FX = 1.0 / (2.0 * math.tan(np.radians(FOV) / 2.0)) * PW
FY = FX
CX = PW / 2.0
CY = PH / 2.0
K = np.asarray([
    [FX, 0, CX],
    [0, FY, CY],
    [0, 0, 1],
])

CAMERA_MATRIX = K
DIST_COEFFS = np.zeros((4, 1))  # no distortion

# prepare: convert to numpy
imagePoints = np.array([
    coord_set[0]
    for coord_set in COORD_SET_FOR_CALIB
], dtype=np.float32)

objectPoints = np.array([
    coord_set[1]
    for coord_set in COORD_SET_FOR_CALIB
], dtype=np.float32)

# estimate Camera Extrinsic Parameter Matrixes
ret, rvec, tvec = cv2.solvePnP(objectPoints, imagePoints, CAMERA_MATRIX, DIST_COEFFS)

print("tvec")
print(tvec)
print("rvec")
print(rvec)

# convert world coordinate to screen coordinate using estimated parameters
imagePointsTest = np.array([
    coord_set[0]
    for coord_set in COORD_SET_FOR_TEST
], dtype=np.float32)

objectPointsTest = np.array([
    coord_set[1]
    for coord_set in COORD_SET_FOR_TEST
], dtype=np.float32)

imgpts, jac = cv2.projectPoints(np.array(objectPointsTest, dtype=np.float32), rvec, tvec, CAMERA_MATRIX, DIST_COEFFS)

print("convert")
print("xyz -> img_pt uv")
for img_pt, uv, xyz in zip(imgpts, imagePointsTest, objectPointsTest):
    print(xyz, "->", img_pt[0], uv)

上のスクリプトを実行すると、以下の結果が得られます。空間の座標（xyz）を変換した値（img_pt）が、画像中の座標（uv）の値と近く、正しく計算できていることがわかります。

tvec
[[   4.14781668]
 [-478.9439016 ]
 [ 300.40721553]]
rvec
[[-0.91335785]
 [ 0.42551559]
 [ 0.78665766]]
convert
xyz -> img_pt uv
[440. 560. 100.] -> [1022.2288   375.87842] [1022.  376.]
[440. 500. 100.] -> [934.34015 452.4143 ] [935. 453.]
[560. 560.  50.] -> [748.4796 353.4154] [748. 354.]
[500. 560.  50.] -> [849.2841  408.35352] [849. 408.]
[560. 500.  50.] -> [661.5087  400.55136] [661. 402.]
[440. 560.  50.] -> [980.516   479.87442] [978. 481.]

２．補足

tvec・rvec と t・R の関係

上記の計算結果を見ると、カメラの座標は x：392, y：336, z：234であるにも関わらず、tvecは[4.14, -478.94, 300.40]であり、異なっているように見えます。これは、OpenCVでは、スクリーン座標とワールド座標を、以下のように計算するように定義しており、tとRの定義が異なっているためです。

http://opencv.jp/opencv-2svn/cpp/camera_calibration_and_3d_reconstruction.html より

なので、これらの値を「０．定義」に合わせるには、上記の式を逆に用いて、以下のように変換すれば良いことになります。（途中、3行1列の回転ベクトルであるrvec、3行3列の回転行列に変換するために、cv2.Rodrigues関数を利用しています）

R_mat, _ = cv2.Rodrigues(rvec)
print("R_mat")
print(R_mat)

R_raw = R_mat.T
t_raw = -R_mat.T @ tvec
print("t_raw")
print(t_raw)
print("R_raw")

R = R_raw
t = t_raw

# convert world coordinate to screen coordinate using estimated parameters
K_inv = np.linalg.inv(K)
print("convert")
print("xyz -> img_pt uv")
for coord_set in COORD_SET_FOR_TEST:
    uv = coord_set[0]
    xyz = coord_set[1]
    xyz_ = np.array(xyz).reshape((3,1))
    uvz_est = K @ R.T @ (xyz_ - t)
    uv_est = uvz_est[0:2] / uvz_est[2]
    # print(f'{x} {y} {z} --> {tuple(map(int, uv_est))} / {uv}')
    print(f'{xyz} --> {uv_est[0][0]}, {uv_est[1][0]} / {uv}')

上記を実行すると、以下の出力を得られます。tの座標も正しく、変換結果もズレが少ないことから、正しく計算できていることがわかります。

R_mat
[[ 0.65163479 -0.75851056  0.00581697]
 [ 0.41998701  0.36717466  0.82993595]
 [-0.63165103 -0.53837208  0.55782836]]
t_raw
[[388.19988066]
 [340.7330847 ]
 [229.89297086]]
R_raw
[[ 0.65163479  0.41998701 -0.63165103]
 [-0.75851056  0.36717466 -0.53837208]
 [ 0.00581697  0.82993595  0.55782836]]
convert
xyz -> img_pt uv
440 560 100 --> 1022.2288237239957, 375.87842361950004 / [1022, 376]
440 500 100 --> 934.3401211342954, 452.41430202598195 / [935, 453]
560 560 50 --> 748.479595104363, 353.4154172638884 / [748, 354]
500 560 50 --> 849.2841405062062, 408.3535277603238 / [849, 408]
560 500 50 --> 661.5087189816594, 400.55134615621046 / [661, 402]
440 560 50 --> 980.5160171168673, 479.8744230647062 / [978, 481]

キャリブレーション用データの選び方

cv2.solvePnPに入力するキャリブレーション用のデータの選び方（キャリブレーションする点の選び方）には注意が必要です。例えば、COORD_SET_FOR_CALIBを以下のように変更した場合です。

COORD_SET_FOR_CALIB = [
    # uvz(screen cood), xyz(unrealengine coord)
    ([663, 306], [560, 500, 100]),
    ([871, 313], [500, 560, 100]),
    ([776, 366], [500, 500, 100]),
    ([758, 263], [560, 560, 100]),
]

COORD_SET_FOR_TEST = [
    # uvz(screen cood), xyz(unrealengine coord)
    ([1022, 376], [440, 560, 100]),
    ([935, 453], [440, 500, 100]),
    ([762, 469], [500, 500, 50]),
    ([898, 562], [440, 500, 50]),
    ([748, 354], [560, 560, 50]),
    ([849, 408], [500, 560, 50]),
    ([661, 402], [560, 500, 50]),
    ([978, 481], [440, 560, 50]),
]

このとき、以下のような出力が得られます。convertした結果、z軸の値が100の点は、正しく変換後のスクリーン座標を推定できているものの、z軸の値が50の点は大きくずれていることがわかります。

tvec
[[  -6.22648339]
 [ 313.70397468]
 [-411.52531089]]
rvec
[[-0.50875648]
 [-1.09355581]
 [-2.06077674]]
convert
xyz -> img_pt uv
[440. 560. 100.] -> [1021.9751  376.5457] [1022.  376.]
[440. 500. 100.] -> [933.7981 453.0137] [935. 453.]
[500. 500.  50.] -> [794.20483 235.69588] [762. 469.]
[440. 500.  50.] -> [983.26447 306.19522] [898. 562.]
[560. 560.  50.] -> [769.71954 156.17647] [748. 354.]
[500. 560.  50.] -> [897.93225 192.55038] [849. 408.]
[560. 500.  50.] -> [665.1294  187.56433] [661. 402.]
[440. 560.  50.] -> [1075.887    243.03615] [978. 481.]
R_mat
[[-0.65058944  0.75941628  0.00450509]
 [-0.42196712 -0.36641731  0.829266  ]
 [ 0.63140885  0.53761071  0.55883593]]
t_raw
[[388.16259923]
 [340.91547261]
 [-30.14085967]]
R_raw
[[-0.65058944 -0.42196712  0.63140885]
 [ 0.75941628 -0.36641731  0.53761071]
 [ 0.00450509  0.829266    0.55883593]]

t_rawを見るとわかるように、UnrealEngineではカメラ座標がz=230ですが、上だとz=-30に推定されています。z=100の点のみを使ってキャリブレーションしたことを考えると、z軸の方向を逆に推定されていることがわかります。

この原因は、キャリブレーション時に同一平面の点のみを使用したことと、今回使用したUnrealEngineの座標系が左手系である（OpenCVは右手系を前提としていて、異なっている）ことです。一般には、正しく一意にカメラ位置を推定するには、同一平面にない6点を用いる必要があります。（詳しい説明は、本記事最後の「参考にさせていただいたページ・サイト」のリンク先などをご参照ください）

ただ、z軸の値が同じ平面の点をャリブレーションに用いていることと、カメラの座標がその平面よりも上（z軸が大きい方）であることを前提とすれば、以下のように補正することができます。（カメラの位置を平面からの距離分を逆方向に加え、回転行列のz軸成分を逆向きにします）

# 書き換える
# R = R_raw
# t = t_raw

# if camera estimation is reversed
t = np.array(t_raw)
R = np.array(R_raw)
Z_CALIB = 100
if t_raw[2] < Z_CALIB:
    t[2] = 2 * Z_CALIB - t[2]
    z_inverse = np.array([
        [1, 0, 0],
        [0, 1, 0],
        [0, 0, -1],
    ])
    R = z_inverse @ R_raw

この状態で、変換させると以下のような出力が得られます。z=50の点も正しく変換できています。

[440, 560, 100] --> 1021.9750900455591, 376.5456915953506 / [1022, 376]
[440, 500, 100] --> 933.7981070806426, 453.0137171293698 / [935, 453]
[500, 500, 50] --> 761.7715230656428, 469.4080388629907 / [762, 469]
[440, 500, 50] --> 896.958677553246, 562.354844723352 / [898, 562]
[560, 560, 50] --> 748.4293201621825, 353.3418175726298 / [748, 354]
[500, 560, 50] --> 849.065086626045, 408.523913776472 / [849, 408]
[560, 500, 50] --> 661.342424147836, 400.3588455781332 / [661, 402]
[440, 560, 50] --> 980.057640613656, 480.3516939993913 / [978, 481]

まとめ

2Dカメラをキャリブレーションするための計算方法をまとめました。また、カメラのパラメータが意図通りではなく推定されてしまった際に補正する方法をまとめました。

参考にさせていただいたページ・サイト

https://www.jstage.jst.go.jp/article/sicejl1962/30/3/30_3_241/_pdf

https://docs.opencv.org/master/d7/d53/tutorial_py_pose.html

https://docs.opencv.org/3.0-beta/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html?highlight=cv2.solvepnp#cv2.solvePnPRansac